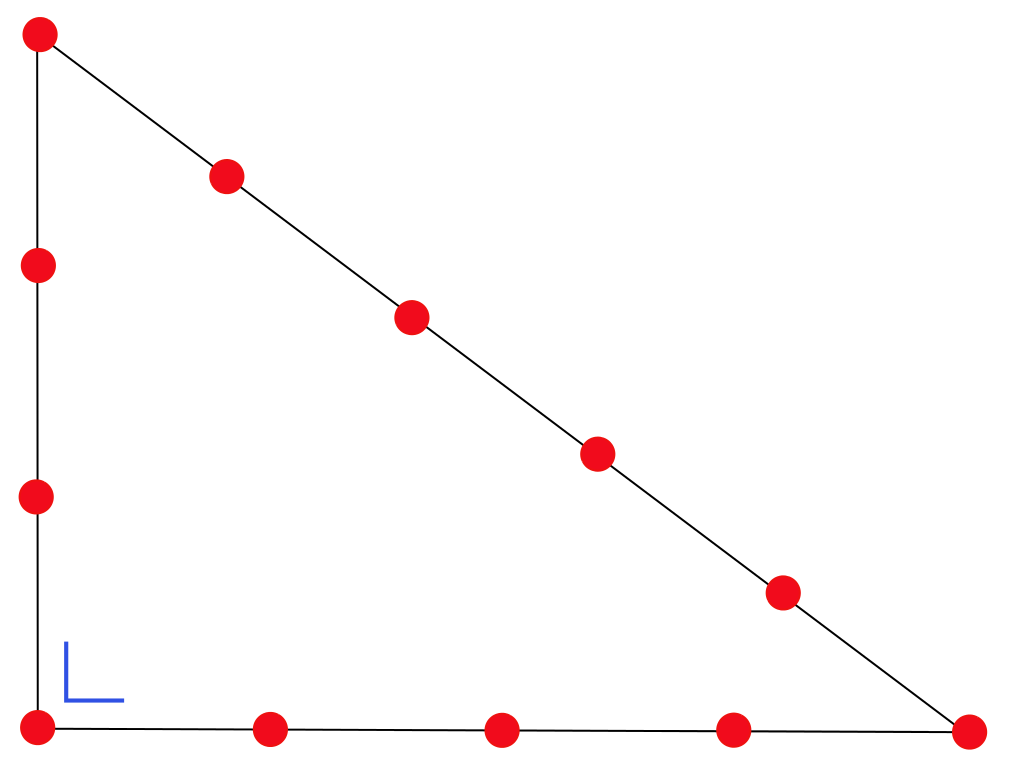
Єгипетський трикутник — прямокутний трикутник зі співвідношенням сторін 3:4:5.

Особливістю такого трикутника, відомою ще з античних часів, є те, що всі його сторони цілочисельні, а згідно з теоремою, оберненою до теореми Піфагора, він є прямокутним. Єгипетський трикутник є найпростішим (і першим відомим) із Геронових трикутників — трикутників з цілочисельними сторонами і площами. Радіус вписаного в трикутник кола рівний одиниці.

Назву трикутнику з таким співвідношенням сторін дали елліни: в VII—V століттях до н. е. грецькі філософи й суспільні діячі активно відвідували Єгипет. Так, наприклад, Піфагор в 535 р. до н. е. за наполяганням Фалеса для вивчення астрономії й математики подався до Єгипту — і, судячи з усього, саме спроба узагальнити співвідношення квадратів, характерне для єгипетського трикутника, на будь-які прямокутні трикутники й привела Піфагора до доведення його знаменитої теореми.

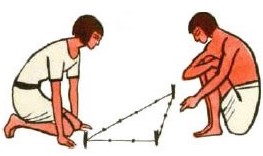Сума зазначених чисел (3+4+5=12) із давніх часів використовувалася як одиниця кратності при побудові прямих кутів за допомогою мотузки, розміченої вузлами на 3/12 й 7/12 її довжини. Застосовувався єгипетський трикутник у середньовічній архітектурі для побудови схем пропорційності^[1]. Сторони єгипетського трикутника утворюють найпростішу піфагорову трійку: 3²+4²=5².

Джерело: Матеріал з Вікіпедії